计算π的历史
圆周率π可能是科学界内外最广为人知的自然常数了。早在公元5世纪时,南朝宋数学家祖冲之用割圆法将圆周率计算到小数点后7位数字。大约同一时间,印度的数学家也将圆周率计算到了小数点后5位。历史上首个π精确无穷级数公式(即莱布尼茨公式)直到约1000年后才由印度数学家发现。20世纪以来,随着计算机技术的快速发展,π的精度也在极速提高。截至2019年,π的十进制精度已高达10^13 位。虽然几乎所有的科学研究对π的精度要求都不会超过几百位,当前依然有许多科学家和爱好者为了打破记录、测试超级计算机的计算能力和高精度乘法算法等原因,不断地向π的更高位数发起挑战。
圆周率有许多优美的数学性质,由此产生的计算圆周率的公式和算法也有成千上万。借《并行计算》实验课的机会,我对其中比较有趣和有意义的一些算法进行了一波研究,实现了代码并进行了一些测试。
方法0:蒲丰投针与蒙特卡洛方法
在介绍蒙特卡洛方法之前,先讲一个概率学上的故事:
在1777年,法国数学家蒲丰(也有译作布丰)设计了一个投针试验,实验方式如下:
1) 取一张白纸,在上面画上许多条间距为a的平行线。
2) 取一根长度为l(l≤a) 的针,随机地向画有平行直线的纸上掷n次,观察针与直线相交的次数,记为m。
3)计算针与直线相交的概率.
蒲丰经过计算,得出这个概率是: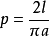 。由此蒲丰惊奇地发现:有利的扔出与不利的扔出两者次数的比,是一个包含π的表示式.如果针的长度等于a/2,那么有利扔出的概率为1/π.扔的次数越多,由此能求出越为精确的π的值。
。由此蒲丰惊奇地发现:有利的扔出与不利的扔出两者次数的比,是一个包含π的表示式.如果针的长度等于a/2,那么有利扔出的概率为1/π.扔的次数越多,由此能求出越为精确的π的值。
一些数学家在这个问题上进行了实验,结果如下:
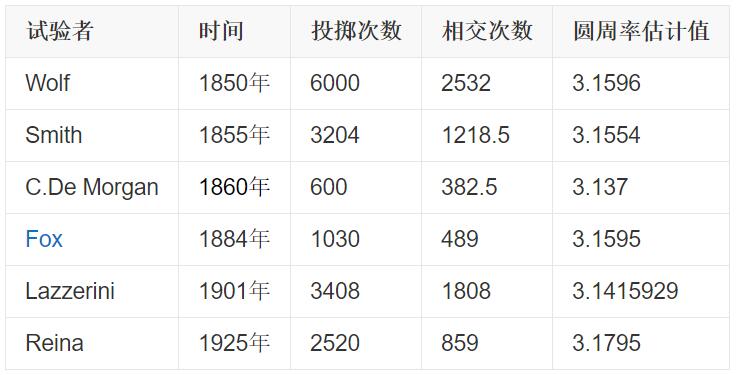
在概率学上,蒲丰投针实验是第一个用几何形式表达概率问题的例子,他首次使用随机实验处理确定性数学问题,为概率论的发展起到了一定的推动作用。
那么在计算机中,我们也可以借鉴蒲丰投针的思想,利用随机事件发生的频率来预估出圆周率的值。当然,由于计算机能够很方便地生成随机数,没有必要使用投针的方式,只需随机生成点就可以计算出圆周率。以下描述一种简单的算法:
首先在(0,1)中生成两个随机数x,y,令(x,y)为坐标系中的一个点,那么它将均匀地分布在(0,0),(1,1)的正方形内。然后统计其中到原点的距离小于1的点的数量。这些点分布在以原点为圆心、半径为1的四分之一个圆上,则其占点的总数的比值的期望为π/4。因此进行多次随机,然后将比值乘以4就可以得到近似的圆周率值。
算法的执行过程如图所示:
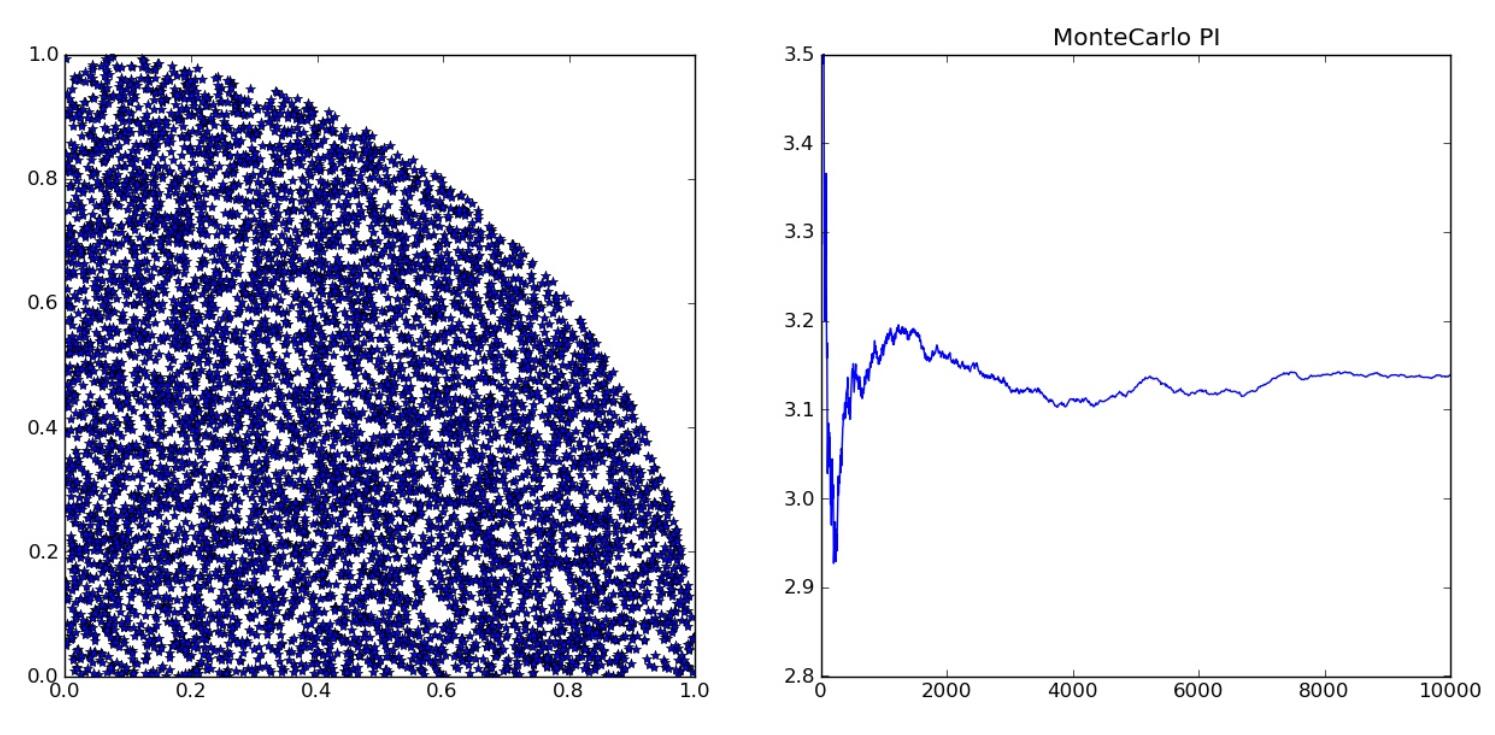
这个算法有一个明显的好处:它天生支持并行或分布式计算,因为每次投掷的试验都是独立的,可以在很多台设备上分别进行随机试验,之后统计结果即可。
方法1:面积积分
上面的方法已经可以在1秒内计算出圆周率的前8位小数,但是如果想要结果更加精确,难度很大。因为这个算法完全依靠随机次数的增加来逼近理论上的概率,而大数定律的收敛很慢。那么既然上面的算法是通过四分之一个单位圆的面积来得到π的值,我们可不可以直接计算圆的面积呢?
由这个思路引出了计算圆周率的第二个方法:利用面积积分。能够得到π的函数很多,因此这个思路得到的算法也不唯一。这里选用了反正切函数y=arctan(x),利用公式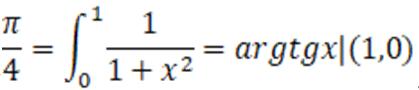 ,可以得到下图中曲线与坐标轴之间围成的面积为π/4。
,可以得到下图中曲线与坐标轴之间围成的面积为π/4。
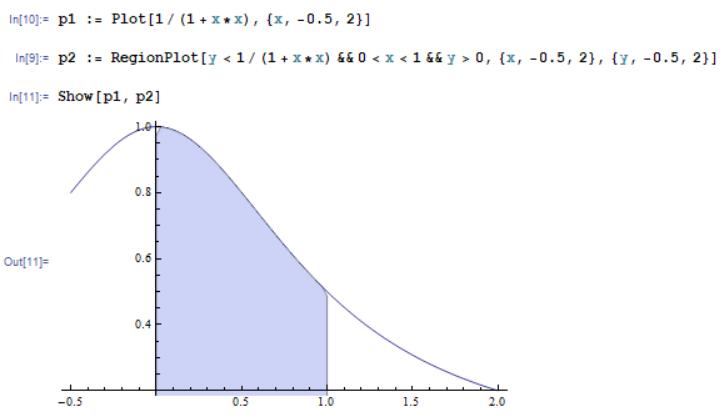
在计算机中,计算图形的面积一般可以用划分+近似为梯形面积+求和的方式来计算。具体算法为:将(0,1)的区间等分为n个部分,如第一部分为(0,1/n]、第二部分为(1/n,2/n]等,然后分别计算x坐标在这个区间范围内对应的图形的面积。由于此时对应的图形很“细”,可以近似地看做一个梯形或一个矩形,则可以套用梯形或矩形的面积计算公式求得结果。最后将这些矩形的面积相加,就得出了不规则图形的面积。可以看出,这个算法的精确程度取决于一开始的划分数量,划分得越细,计算的精确度就越高。
同时这个算法也支持并行计算:在程序的开始对梯形的划分进行预分配,然后各个进程分别计算自己被分配到的梯形的面积,最后在进行求和即可。
并行程序的代码如下:
#include "mpi.h"
#include <stdio.h>
#include <math.h>
double f(double);
double f(double a)
{
return (4.0 / (1.0 + a * a));
}
int main(int argc, char *argv[])
{
int n, myid, numprocs, i;
double PI25DT = 3.141592653589793238462643;
double mypi, pi, h, sum, x;
double startwtime = 0.0, endwtime;
int namelen;
char processor_name[MPI_MAX_PROCESSOR_NAME];
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &numprocs);
MPI_Comm_rank(MPI_COMM_WORLD, &myid);
MPI_Get_processor_name(processor_name, &namelen);
fprintf(stdout, "Process %d of %d is on %s\n", myid, numprocs, processor_name);
fflush(stdout);
n = 10000; /* default # of rectangles */
if (myid == 0)
startwtime = MPI_Wtime();
MPI_Bcast(&n, 1, MPI_INT, 0, MPI_COMM_WORLD);
h = 1.0 / (double) n;
sum = 0.0;
/* A slightly better approach starts from large i and works back */
for (i = myid + 1; i <= n; i += numprocs) {
x = h * ((double) i - 0.5);
sum += f(x);
}
mypi = h * sum;
MPI_Reduce(&mypi, &pi, 1, MPI_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
if (myid == 0) {
endwtime = MPI_Wtime();
printf("pi is approximately %.16f, Error is %.16f\n", pi, fabs(pi - PI25DT));
printf("wall clock time = %f\n", endwtime - startwtime);
fflush(stdout);
}
MPI_Finalize();
return 0;
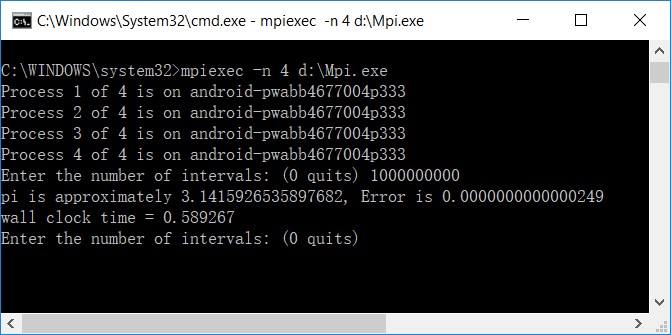
}在单机4进程的并行环境下运行程序的结果如下图所示。可以看到,经过1e9次分割,误差2.49e-14,耗时0.589267秒,计算速度约为27位/秒。
方法2:幂级数
除了利用将函数积分转化为分段求和的方式来逼近圆周率之外,数学上还有不少可以用来计算π的公式,比如利用幂级数对arctan(x)进行展开可以得到:
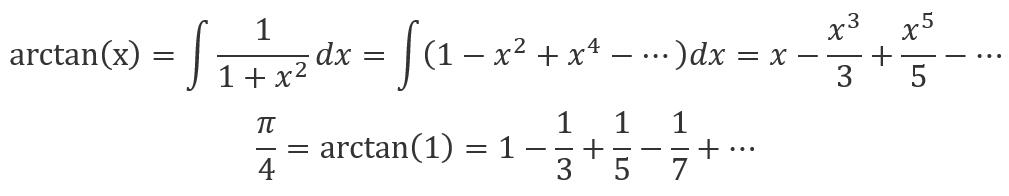
对这个式子进行简单的循环求和,也可以逐渐逼近圆周率的值。
同时这种方法也可以实现并行计算,首先由主节点确定要计算的项数,将计算任务分配到各个节点,然后上多个节点可以分别计算式子的不同部分,然后将结果相加即可。
以下是这种方法的代码:
#include "mpi.h"
#include <stdio.h>
#include <math.h>
long double f(long long a)
{
return ((a&1)?4.0L:-4.0L)/(a+a-1);
}
int main(int argc, char *argv[])
{
int myid, numprocs, done = 0;
long long n, i;
long double PI25DT = 3.141592653589793238462643;
long double mypi, pi, h, sum, x;
double startwtime = 0.0, endwtime;
int namelen;
char processor_name[MPI_MAX_PROCESSOR_NAME];
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &numprocs);
MPI_Comm_rank(MPI_COMM_WORLD, &myid);
MPI_Get_processor_name(processor_name, &namelen);
fprintf(stdout,"Process %d of %d is on %s\n",
myid+1, numprocs, processor_name);
fflush(stdout);
while(!done) {
if(myid == 0) {
fprintf(stdout, "Enter the number of iterations: (0 quits) ");
fflush(stdout);
if(scanf("%lld", &n) != 1) {
fprintf(stdout, "No number entered; quitting\n");
n = 0;
}
startwtime = MPI_Wtime();
}
MPI_Bcast(&n, 1, MPI_LONG_LONG, 0, MPI_COMM_WORLD);
if(n == 0)
done = 1;
else {
sum = 0.0;
for(i = myid + 1; i <= n; i += numprocs) {
sum += f(i);
}
mypi = sum;
MPI_Reduce(&mypi, &pi, 1, MPI_LONG_DOUBLE, MPI_SUM, 0, MPI_COMM_WORLD);
if(myid == 0) {
printf("pi is approximately %.16f, Error is %.16f\n",
pi, fabs(pi - PI25DT));
endwtime = MPI_Wtime();
printf("wall clock time = %f\n", endwtime-startwtime);
fflush(stdout);
}
}
}
MPI_Finalize();
return 0;
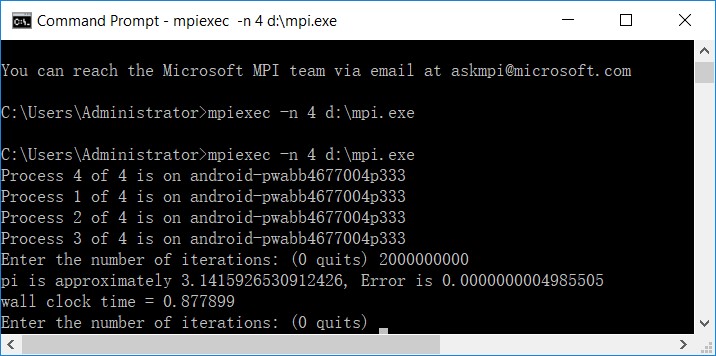
}在单机4进程的并行环境下运行程序的结果如下图所示。可以看到,经过2e9次分割,误差4.98e-10,耗时0.877899秒,计算速度约为14位/秒。
方法3:改进的幂级数
以上两种方法本质上都是通过逼近一个极限为π的数列来计算圆周率的。上面的两个数列每一项衰减得比较慢,要精确到10^-N^ 大致需要计算2*10^N^项。^^
对于幂级数而言,当x越接近于0时,收敛越快。比如在上面的例子中,我们选取的x=1,离0有相当的距离。如果对arctan(x)在x=1/5处展开,可以得到级数:
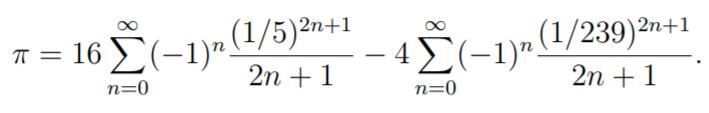
以上级数由于含有1/5和1/239的指数运算,收敛速度很快。事实上,当n=4时,就有1/9*5^9^ <10^-6^ ;而右边收敛的更快。
采用和方法2相似的并行计算方式,我们就可以很快地计算圆周率了。从这种方法开始,由于计算出的圆周率的精度远超double或long double的精度,为了测试这种方案的效率上限,我使用了boost库中的multiprecision::cpp_bin_float这个高精度 库,用来进行高精度数字的计算。该高精度库使用了FFT加速的大数乘法等运算,效率较高。
由于高精度的变量类型不在Mpi的基本变量类型范围内,因此改用了Mpi_Gather函数对其进行收集后手动叠加。此外,由于高精度场景下加法、乘法、除法等运算的复杂度不再是O(1),导致求和式中的每一项的计算所需的时间复杂度 也不相同。因此并行时采用了均摊的思想,每个程序计算第(i+nk)项,其中i为程序的rank,n为线程数量,k为正整数。
本方法的代码如下:
#include "mpi.h"
#include <iostream>
#include <fstream>
#include <math.h>
#include <boost/multiprecision/cpp_bin_float.hpp>
using namespace boost::multiprecision;
#define PRECISION 2000
typedef number<cpp_bin_float<PRECISION> > pi_type;
typedef int a_type;
pi_type f(a_type a)
{
return ((a&1)?pi_type(16):pi_type(-16))/(a+a-1)/pow(pi_type(5),a+a-1) -
((a&1)?pi_type(4):pi_type(-4))/(a+a-1)/pow(pi_type(239), a+a-1);
}
pi_type pi_exact;
int main(int argc, char *argv[])
{
std::ifstream fin("d:\\pi.txt");
char buf[PRECISION+2];
fin.get(buf, PRECISION+1);
pi_exact = pi_type(buf);
// 从文件读入Pi的精确值,用于计算精度。
int myid, numprocs, done = 0, namelen;
double startwtime = 0.0, endwtime;
char processor_name[MPI_MAX_PROCESSOR_NAME];
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &numprocs);
MPI_Comm_rank(MPI_COMM_WORLD, &myid);
MPI_Get_processor_name(processor_name, &namelen);
fprintf(stdout,"Process %d of %d is on %s\n",
myid+1, numprocs, processor_name);
fflush(stdout);
while(!done) {
a_type n, i;
if(myid == 0) {
fprintf(stdout, "Enter the number of iterations: (0 quits) ");
fflush(stdout);
std::cin >> n;
startwtime = MPI_Wtime();
}
MPI_Bcast(&n, sizeof(n), MPI_BYTE, 0, MPI_COMM_WORLD);
if(!n)
done = 1;
else {
pi_type pi=0, sum=0;
for(i = myid + 1; i <= n; i += numprocs) {
sum += f(i);
}
pi_type *in = NULL;
if(myid == 0) {
in = (pi_type*)malloc(sizeof(pi_type)*numprocs);
}
MPI_Gather(&sum, sizeof(sum), MPI_BYTE, in, sizeof(sum), MPI_BYTE, 0, MPI_COMM_WORLD);
if(myid == 0) {
for(int i=0; i<numprocs; i++){
pi += in[i];
}
std::cout << std::defaultfloat << std::setprecision(PRECISION);
std::cout << "pi is approximately " << pi << std::endl;
std::cout << std::scientific << std::setprecision(5);
std::cout << "Error is " << boost::multiprecision::fabs(pi - pi_exact) << std::endl;
/*printf("pi is approximately %.16f, Error is %.16f\n", pi, fabs(pi - pi_exact));*/
endwtime = MPI_Wtime();
printf("wall clock time = %f\n", endwtime-startwtime);
fflush(stdout);
}
}
}
MPI_Finalize();
return 0;
}在单机4进程的并行环境下运行程序的结果如下图所示。可以看到,经过1600次迭代,误差1.17666e-1999,耗时1.6秒,计算速度约为1250位/秒。
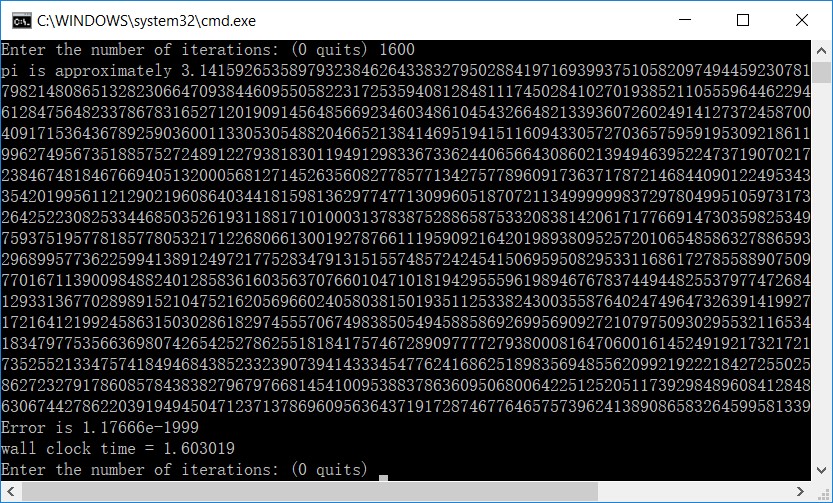
进行了更多数据的测试,结果如下:
720次循环,误差为6.28261e-999(精确到1000位),花费时间0.503472秒。
1440次循环,误差为1.17666e-1999(精确到2000位),花费时间1.447734秒。
2160次循环,误差为5.76950e-2999(精确到3000位),花费时间为4.64656秒。
3500次循环,误差为6.62508e-5000(精确到5000位),花费时间为24.713461秒。
通过测试结果可以看出,随着循环次数的增多,循环次数(级数的累加次数)与圆周率计算的位数呈线性增长,增长率约为0.72(循环/位)。但可能是由于高精度运算比较耗时,如对高精度的指数、除法等运算的复杂度较高,可以看到随着位数的增加,运行时间的增长非常迅速,可能为O(n^3^ )。因此使用这个方法来计算更多位数的圆周率比较困难。
方法4:BBP公式
以上这些圆周率计算方法都是基于简单的数学结论,已经能够获得不错的计算结果,但还有很大的改进空间。随着人们对计算圆周率更高位数的不断追求,其算法也在不断地被发明和改进。这个链接给出了一个圆周率位数的世界纪录年表,可以在这里看到各位前辈在这个问题下做出过的努力:Chronology of computation of π。下面研究并介绍了其中的几个典型的“超级圆周率算法”。
BBP公式,全称Bailey–Borwein–Plouffe formula ,发现于1995年,以三位发表者的名字命名。
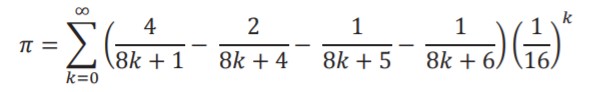
这个公式的特殊之处就在于公式中的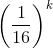 。式子的前半部分是一个单调递减、极限为0的式子,这意味着对于任意正整数k,求和式的第k+1项起每项都(远)小于
。式子的前半部分是一个单调递减、极限为0的式子,这意味着对于任意正整数k,求和式的第k+1项起每项都(远)小于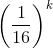 。这个性质使得该算法有一个非常神奇的特点:它可以跳过圆周率前面的位数直接计算目标位数,比如直接计算圆周率的第100000位,而不用耗费内存来存储和计算前99999位数字。
。这个性质使得该算法有一个非常神奇的特点:它可以跳过圆周率前面的位数直接计算目标位数,比如直接计算圆周率的第100000位,而不用耗费内存来存储和计算前99999位数字。
若想要计算圆周率的第n位(此处指十六进制下的第n位,后面会考虑如何计算十进制),对该公式进行如下变形:
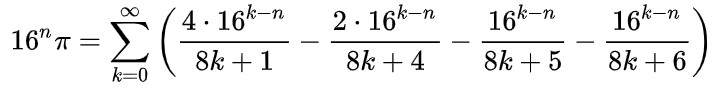
然后计算右边的小数部分。其中右半部分可以写成:
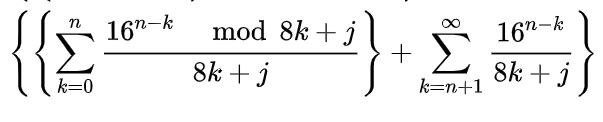
其中mod指求余运算。这样,前半部分可以使用快速幂算法加速运算,复杂度为O(n*log(n));后半部分收敛速度很快,可以通过计算循环的前100项来代替。所以整个过程的复杂度为O(n^2^ log(n))。
该算法的源论文地址为:math.CA/9803067。
由于本算法是基于分别计算圆周率的各位数码,因此很适合改造为并行计算。在实验中我首先实现了BBP算法,然后将其改造成了相应的并行计算程序。
在细节处理方面,其中值得注意的是对运算结果进行按照16进制取模的过程中,为了保证其浮点数存储没有误差(因为分段运算,一点点误差都会导致后面的数值白算),先后尝试了两种方法:
double solve(int id){
double res, series(int, int);
res = 4.*series(1, id) - 2.*series(4, id) - series(5, id) - series(6, id);
res = res - floor(res);
///方法一
//auto temp = (*((long long*)(&res)))&0xFFFFFFFFFFF00000L;
//return *(double*)&temp;
//方法二
return floor(res*4294967296.l)/4294967296.0;
}第一种方法是对double进行截断,即根据C++中浮点数的存储规则,对其超出精度的部分进行截取,相当于在16进制下对16^-9取模;另一种方法是利用floor函数进行截断。经过试验,第二种方法比较稳定,在计算到10000位时都没有遇到问题,而第一种方法会产生误差。
以下是BBP程序的完整代码:
#include "mpi.h"
#include <iostream>
#include <fstream>
#include <math.h>
#include <boost/multiprecision/cpp_bin_float.hpp>
using namespace boost::multiprecision;
#define PRECISION 10000
typedef number<cpp_bin_float<PRECISION> > pi_type;
typedef int a_type;
double solve(int id){
double res, series(int, int);
res = 4.*series(1, id) - 2.*series(4, id) - series(5, id) - series(6, id);
res = res - floor(res);
//auto temp = (*((long long*)(&res)))&0xFFFFFFFFFFF00000L;
//return *(double*)&temp;
return floor(res*4294967296.l)/4294967296.0;
}
double series(int m, int id)
/* This routine evaluates the series sum_k 16^(id-k)/(8*k+m)
using the modular exponentiation technique. */
{
int k;
double ak, eps=1e-17, p, s=0, t, expm(double, double);
/* Sum the series up to id. */
for(k = 0; k < id; k++){
ak = 8 * k + m;
p = id - k;
t = expm(p, ak);
s = s + t / ak;
s = s - (int)s;
}
/* Compute a few terms where k >= id. */
for(k = id; k <= id + 100; k++){
ak = 8 * k + m;
t = pow(16., (double)(id - k)) / ak;
if(t < eps) break;
s = s + t;
s = s - (int)s;
}
return s;
}
double expm(double p, double ak)
/* expm = 16^p mod ak. This routine uses the left-to-right binary
exponentiation scheme. */
{
int i, j;
double p1, pt, r;
#define ntp 25
static double tp[ntp];
static int tp1 = 0;
/* If this is the first call to expm, fill the power of two table tp. */
if(tp1 == 0) {
tp1 = 1;
tp[0] = 1.;
for(i = 1; i < ntp; i++) tp[i] = 2. * tp[i-1];
}
if(ak == 1.) return 0.;
/* Find the greatest power of two less than or equal to p. */
for(i = 0; i < ntp; i++) if(tp[i] > p) break;
pt = tp[i-1];
p1 = p;
r = 1.;
/* Perform binary exponentiation algorithm modulo ak. */
for(j = 1; j <= i; j++){
if(p1 >= pt){
r = 16. * r;
r = r - (int)(r / ak) * ak;
p1 = p1 - pt;
}
pt *= .5;
if(pt >= 1.){
r = r * r;
r = r - (int)(r / ak) * ak;
}
}
return r;
}
pi_type pi_exact;
int main(int argc, char *argv[])
{
std::ifstream fin("d:\\pi.txt");
char buf[PRECISION+2];
fin.get(buf, PRECISION+1);
pi_exact = pi_type(buf);
// 从文件读入Pi的精确值,用于计算精度。
int myid, numprocs, done = 0, namelen;
double startwtime = 0.0, endwtime;
char processor_name[MPI_MAX_PROCESSOR_NAME];
MPI_Init(&argc, &argv);
MPI_Comm_size(MPI_COMM_WORLD, &numprocs);
MPI_Comm_rank(MPI_COMM_WORLD, &myid);
MPI_Get_processor_name(processor_name, &namelen);
fprintf(stdout,"Process %d of %d is on %s\n",
myid+1, numprocs, processor_name);
fflush(stdout);
while(!done) {
a_type n, i;
if(myid == 0) {
fprintf(stdout, "Enter the number of iterations: (0 quits) ");
fflush(stdout);
std::cin >> n;
n = n*log(10)/log(16);
startwtime = MPI_Wtime();
}
MPI_Bcast(&n, sizeof(n), MPI_BYTE, 0, MPI_COMM_WORLD);
if(!n)
done = 1;
else {
pi_type pi=3, sum=0;
for(i = myid*8; i < n; i += numprocs*8) {
auto j=pow(pi_type(1/16.), i)*solve(i);
//std::cout << std::scientific << std::setprecision(30) << j << std::endl;
sum += j;
}
pi_type *in = NULL;
if(myid == 0) {
in = (pi_type*)malloc(sizeof(pi_type)*numprocs);
}
MPI_Gather(&sum, sizeof(sum), MPI_BYTE, in, sizeof(sum), MPI_BYTE, 0, MPI_COMM_WORLD);
if(myid == 0) {
for(int i=0; i<numprocs; i++){
pi += in[i];
}
std::cout << std::defaultfloat << std::setprecision(PRECISION);
std::cout << "pi is approximately " << pi << std::endl;
std::cout << std::scientific << std::setprecision(5);
std::cout << "Error is " << boost::multiprecision::fabs(pi - pi_exact) << std::endl;
/*printf("pi is approximately %.16f, Error is %.16f\n", pi, fabs(pi - pi_exact));*/
endwtime = MPI_Wtime();
printf("wall clock time = %f\n", endwtime-startwtime);
fflush(stdout);
}
}
}
MPI_Finalize();
return 0;
}程序的运行截图如下:
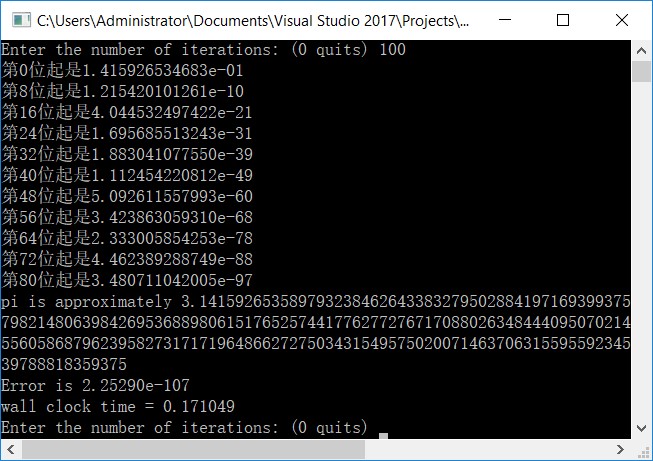
测试结果:
计算到1000位,所需时间0.812535秒;
计算到2000位,所需时间1.839296秒;
计算到5000位,所需时间5.365835秒;
计算到10000位,所需时间14.599410秒。
可以看出,用这种方法计算圆周率的效果较好,速度增长率接近线性(慢于线性的原因猜测是内存开销变大和高精度操作导致的缓慢),而且很短时间内计算出了前10000位的数值。
此外,这种方法的一个显著优点是它可以从圆周率的中间开始计算,如直接算出圆周率的第100000位而不需要知道前面的数字,既能很方便地转化为并行计算,又能提供一种计算圆周率较高位数的捷径。
阅读参考资料得知,这种算法可以被用于验证圆周率的超高位数计算的结果是否正确,方法是利用其直接计算某一位的性质,对计算结果进行随机抽测。
方法5: Chudnovsky 算法
Chudnovsky 算法在1988年被乔纳斯基兄弟发明,是至今圆周率计算位数世界纪录保持者使用的算法。Google Cloud在2018年九月-2019年一月的五个月里,用该算法计算出了圆周率的前31.4兆位小数。
该算法的详细证明可参见这篇论文:JSTOR 40391165。它基于这个收敛速度极快的广义超几何级数:
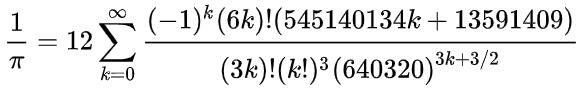
对式子进行化简,使其便于计算机计算,可以得到:
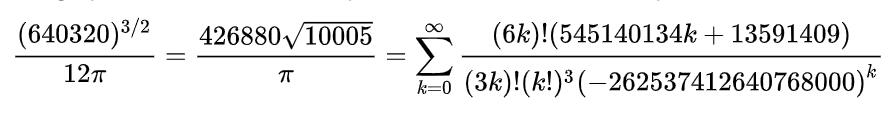
因此算法可以写作一个迭代式:
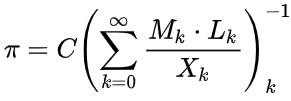
其中
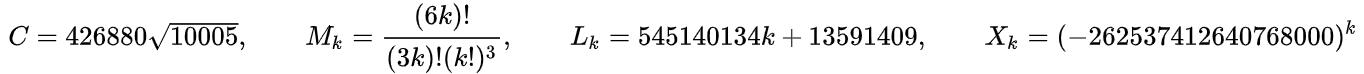
由于算法基于迭代,难以并行化。因此简单地对该算法实现了非并行的代码如下:
#include "mpi.h"
#include <iostream>
#include <fstream>
#include <math.h>
#include <Windows.h>
#include <boost/multiprecision/cpp_bin_float.hpp>
using namespace boost::multiprecision;
#define PRECISION 25000
typedef number<cpp_bin_float<PRECISION> > pi_type;
typedef int a_type;
const int ITER=2400;
pi_type pi, pi_exact;
int main(int argc, char *argv[])
{
std::ifstream fin("d:\\pi.txt");
char buf[PRECISION+2];
fin.get(buf, PRECISION+1);
pi_exact = pi_type(buf);
// 从文件读入Pi的精确值,用于计算精度。
double startwtime = clock(), endwtime;
long long K=6, L=13591409;
pi_type M=1, X=1, S=13591409;
for(int i=1; i<=ITER; i++){
M = floor((pow(K, 3)-16*K)*M/pow(i,3));
L += 545140134;
X *= -262537412640768000.l;
S += M * L / X;
K += 12;
// std::cout<<M<<" "<<X<<" "<<S<<std::endl;
}
pi = 426880 * sqrt(pi_type(10005)) / S;
std::cout << std::defaultfloat << std::setprecision(PRECISION);
std::cout << "pi is approximately " << pi << std::endl;
std::cout << std::scientific << std::setprecision(5);
std::cout << "Error is " << boost::multiprecision::fabs(pi - pi_exact) << std::endl;
/*printf("pi is approximately %.16f, Error is %.16f\n", pi, fabs(pi - pi_exact));*/
endwtime = clock();
printf("wall clock time = %f s\n", (endwtime-startwtime)/1000.);
system("pause");
return 0;
}程序的运行截图如下:
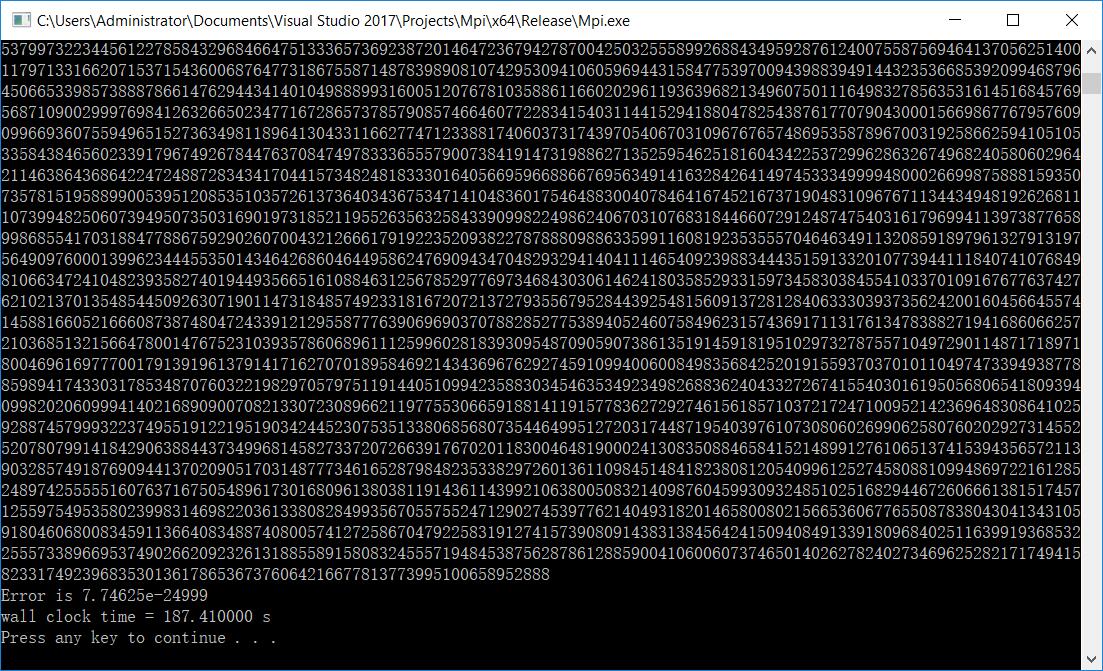
该算法在三分钟左右计算出了圆周率的前25000位结果。由于这是在单核单进程的运行环境下进行的运算,达到这样的效率,比起BBP算法又是进步了不少。
事实上,虽然该算法从逻辑上难以并行化,但查阅资料得知,大整数乘法的FFT运算本身其实是可以并行化的,甚至可以放在GPU、TPU等设备中进行加速运算,达到更高的计算速度。如果以后有机会在这些设备上编程时,也许我会想办法在上面写一个Chudnovsky 算法,测测看它们的性能。
结论
经过这些实验可以发现,同样一个计算圆周率的问题,不同的数学原理得出了不同的算法,其结果和速度也会天差地别。
同时,随着计算位数的提升,不仅是公式的收敛速度、算法的时间复杂度在限制着计算的速度,高精度运算的时间消耗、内存消耗也开始出现瓶颈。查看世界纪录计算数亿上兆位圆周率的计算报告可知,在更高位数上计算时,RAM、Cache、磁盘、RAID、cpu指令集等因素也对结果有很大影响,都被优化到了极致。
此外,通过这次实验我也体会到了并行计算的强大之处:从蒙特卡洛算法到积分分割,再到级数计算和BBP算法计算数码,各种不同的算法通过各种方式被并行化,多个节点分别计算部分任务,然后再Gather到主节点上,达到了数倍的性能提升。
算法的优化是永无止境的。对圆周率这个超越数的探索过程,也是对计算机计算能力的探索过程。从公式、算法到并行计算、硬件优化,也许这就是圆周率计算的魅力所在吧!
参考资料
- 《并行计算实验指导书——圆周率π的计算》 – 北邮软件学院 卢本捷
- 那些打破圆周率小数位计算的记录是怎么判断计算得正不正确的? - 知乎 酱紫君
- Pi Formulas, Algorithms and Computations - Fabrice Bellard
- 圆周率 - Wikipedia
- BBP Formula - Wikipedia
- 用计算机算圆周率,是个怎样的过程? - 知乎

此处评论已关闭