机器学习介绍
算法的类型
Supervised: 对已经标记的数据进行训练以预测标签。
- Self-supervised: 标签是从数据生成的 (例如: word2vec、BERT)
- Semi-supervised: 对标记和未标记数据进行训练,学习模型以预测标签或推断未标记数据的标签。
- Unsupervised: 对未标记数据进行训练。例如: 聚类、密度估计 (GAN)
- Reinforcement: 利用与环境互动的观察结果采取行动,最大限度地提高奖励 (类似人类的学习过程,较难)
监督学习
- 模型:从输入预测输出。如: 挂牌房屋-售价
- 损失函数:测量预测与真实标签之间的差异。例如 (预测价格-销售价格)^2
- 目标:训练过程中需要优化的任何函数。例如:最小化损失
- 优化:学习模型参数
监督模型的类型
决策树、线性方法、核方法、神经网络
决策树
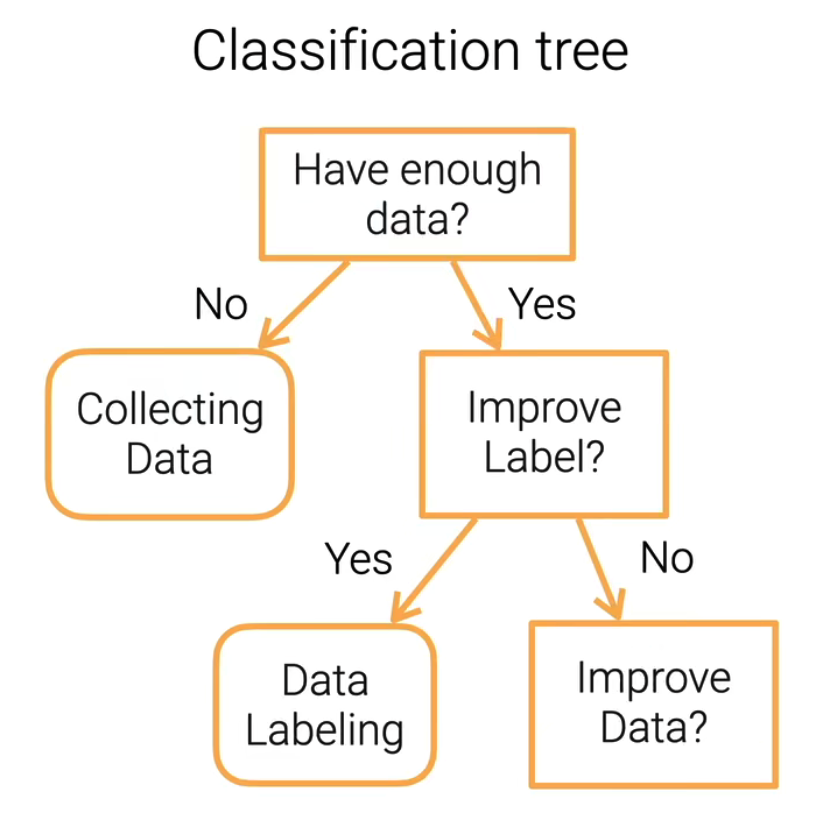
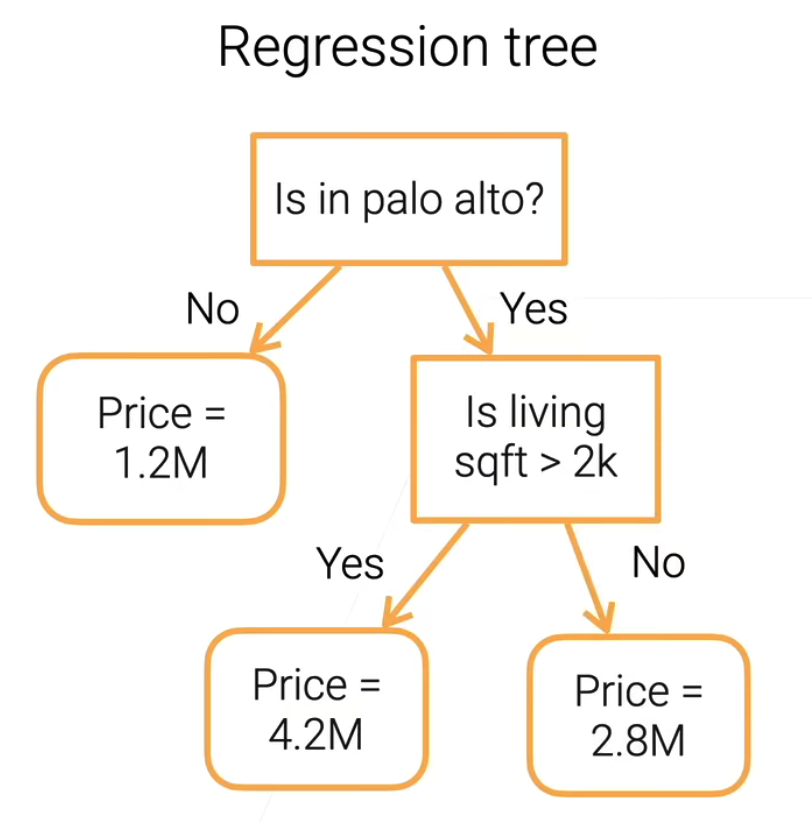
决策树
好处
- 可解释性
- 可以处理数字和类别特征
坏处
- 非常不稳定,容易被噪声影响 (集成学习帮助)
- 复杂的树导致过拟合 (修剪树)
- 在计算中不容易被并行化
随机森林
为了改善不稳定的缺点。一棵树不行就训练多棵树。
训练多个决策树以提高鲁棒性。
- 每棵树都是独立训练的
- 分类 → 投票,回归 → 平均
为什么是随机呢?
- 有放回的随机采样,可能会有重复。例如:
[1,2,3,4,5]→[1,2,2,3,4] - 随机选择特征子集
- 有放回的随机采样,可能会有重复。例如:
梯度Boosting决策树
- 顺序训练多棵树
$t$ 表示时间, $F_t(x)$ 表示过去训练所有树输出的和
- 在没有做好预测的那部分(残差)里训练一个新树 $f_t$ ,如果$[x_i,y_i-F_t(x_i)]_i...$ 在减小,证明新树靠谱。
- $F _ { t + 1 } ( x ) = F _ { t } ( x ) + f _ { t } ( x ) $
- 使残差去拟合负梯度 $[x_i,y_i-F_t(x_i)]_i = - \partial L / \partial F $
总结
- 决策树: 分类/回归的可解释模型
减少偏差和方差的树
- 随机森林: 随机性并行训练
- 梯度提升树: 在残差上顺序训练
决策树在工业中被广泛使用
- 简单,易于调整,通常会给出满意的结果
线性模型
线性模型
一个简单的房价预测模型
- 假设 $x_1,x_2,x_3$是三个可以影响房价的因素(特征)
- 那么,预测的价格为:$y=w_1x_1+w_2x_2+w_3x_3+b$
- 权重 $w_1,w_2,w_3$ 和偏移量 $b$ 可以从训练的数据中得到
- 代码表示

目标函数
最小化均方误差(MSE)
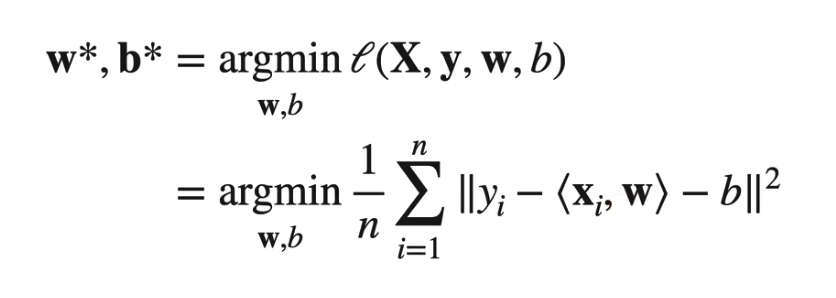
使用线性回归进行分类
- 回归: 连续输出 (R)
分类:
- 为每一个类学习一个模型
- 为标签应用
one-hot编码,$y=[y_1,y_2,...,y_m]$ 如果$i=y$ 那么,$y_i=1$ - 最小化 MSE 损失
- 预测标签 $argmax_i{o_i}^m$
Softmax Regression
- Softmax: 输出的分数转概率 $\hat{y}_{i}=\frac{\exp \left(o_{i}\right)}{\sum_{k=1}^{m} \exp \left(o_{k}\right)}$
交叉熵损失函数:$H(\mathbf{y}, \hat{\mathbf{y}})=\sum_{i}-y_{i} \log \left(\hat{y}_{i}\right)=-\log \hat{y}_{y}$
最小化 $-\log \hat{y}_{y}$ ,最大化 $\log \hat{y}_{y}$
只关注该样本真实类别上预测的概率是多少

此处评论已关闭